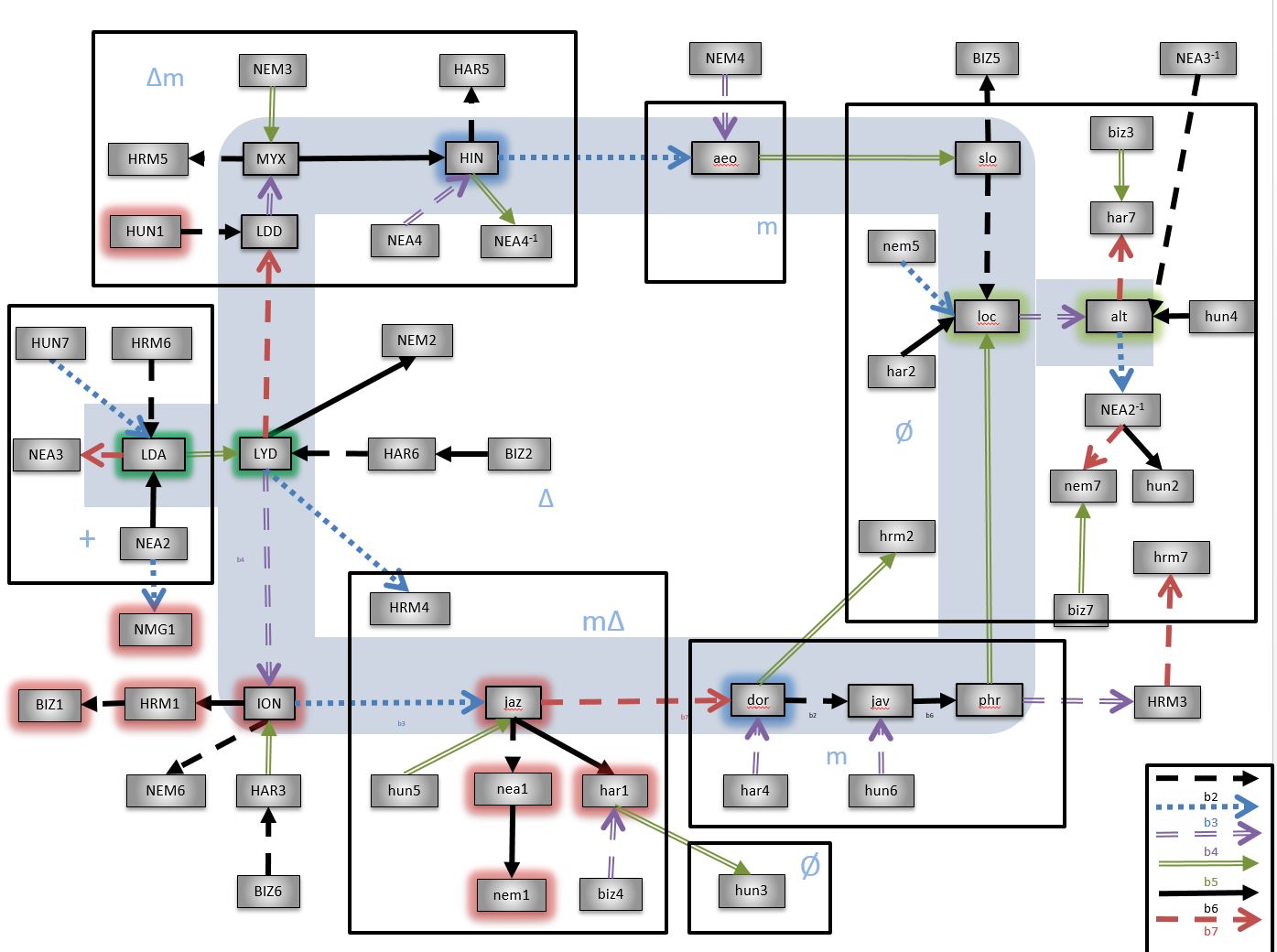
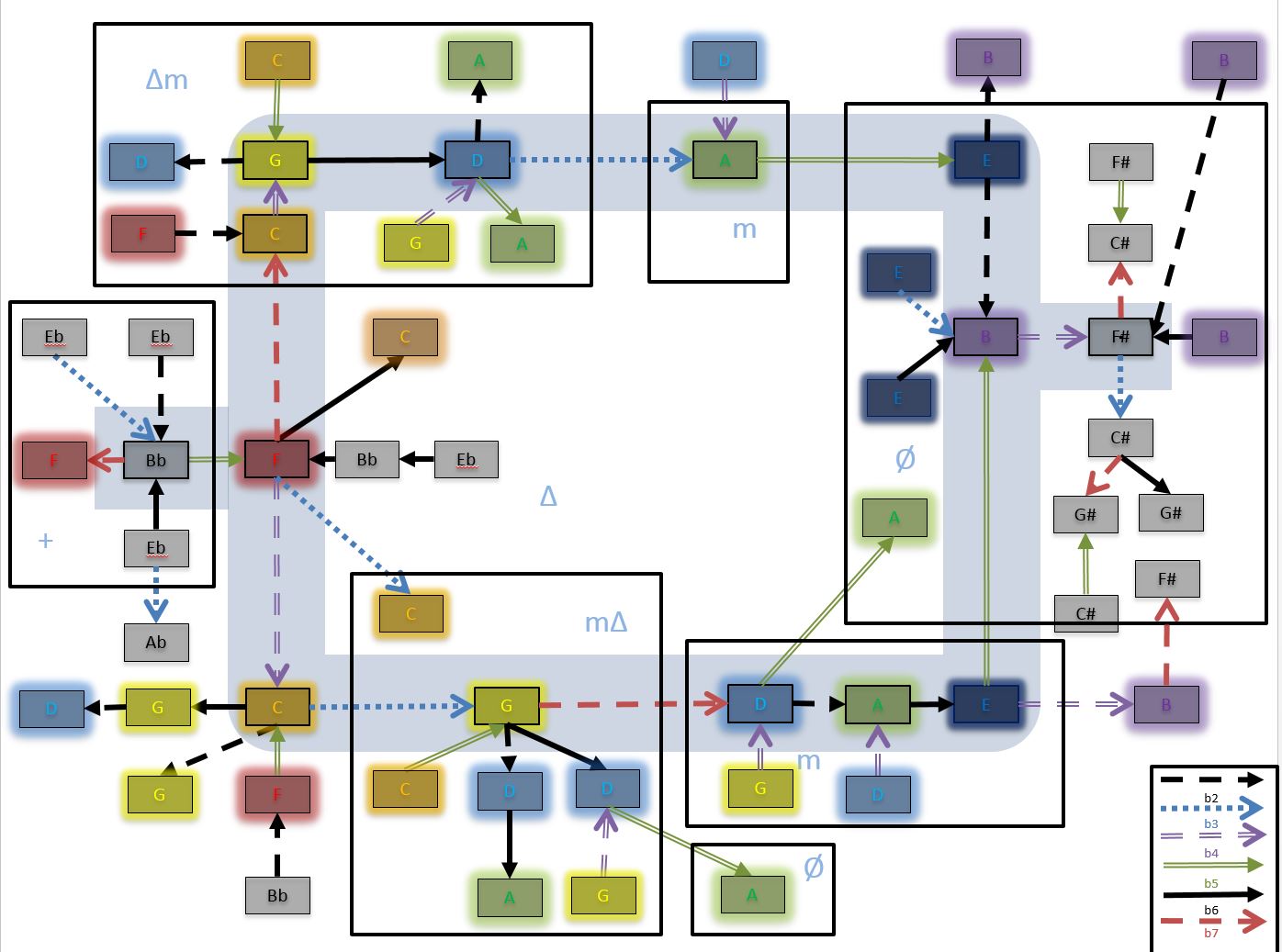
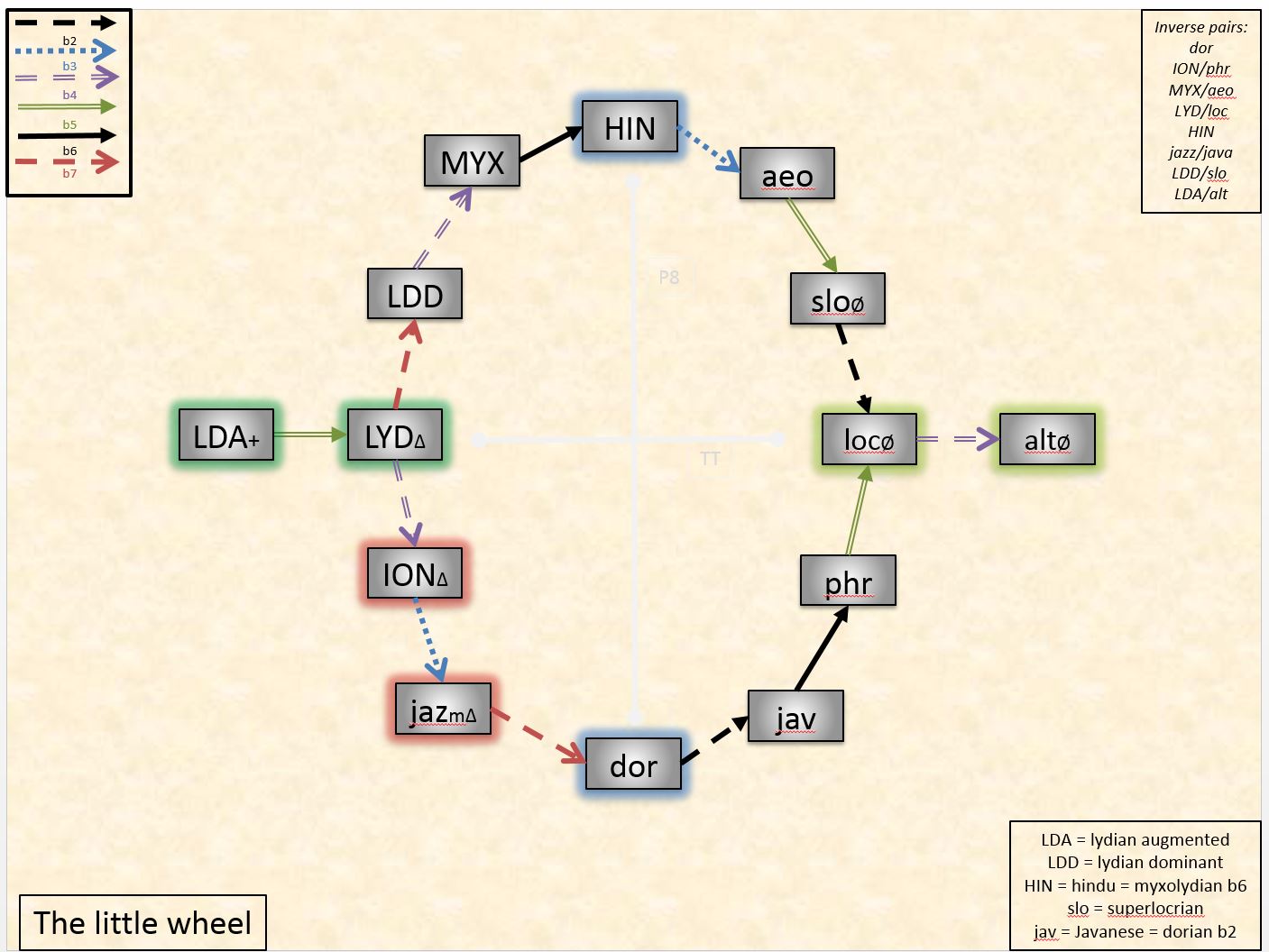
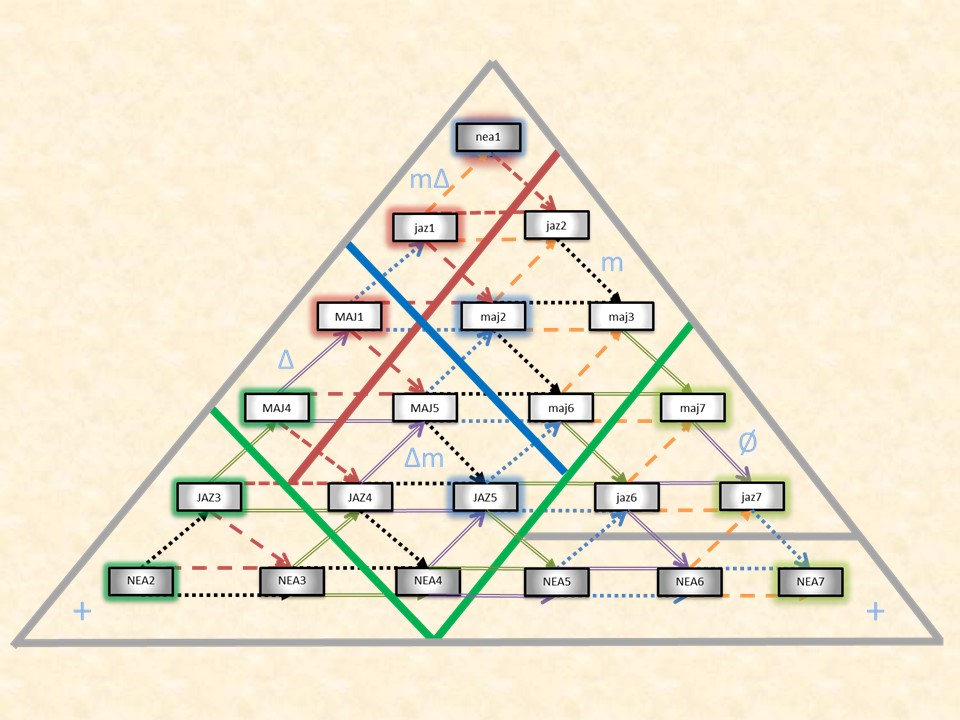
- An accidental network is a graph with modes as vertices and jumps as directed edges. There are two main types of accidental networks, modal rings and modal wheels.
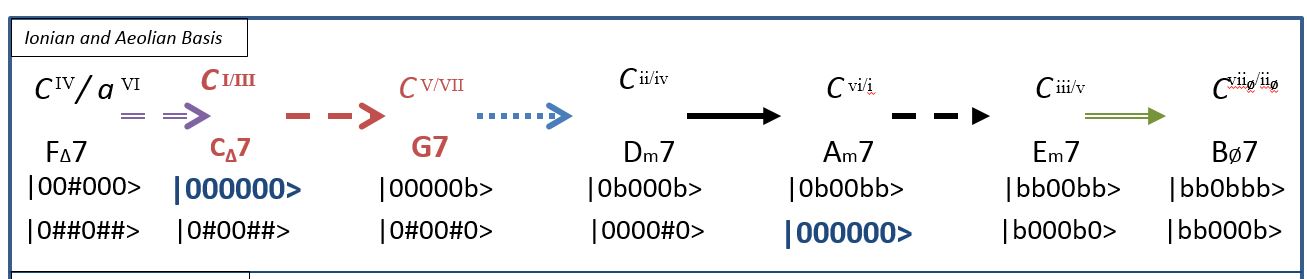
Each mode has a unique collection of flat and sharp accidentals relative to ionian that define that mode. This concept was explored in the accidental abacus where we also saw that remaining diatonic required a very specific perfect fifth key center change, a jump. In an accidental network, these jumps are modeled as arrows that connect modes to form chains of modes or networks. And while there is a mathematical foundation to the accidental network (which can be explored at www.chromaticgrouptheory.com), for orijikan it is enough to associate an accidental network with its visualization:
AN diagram.
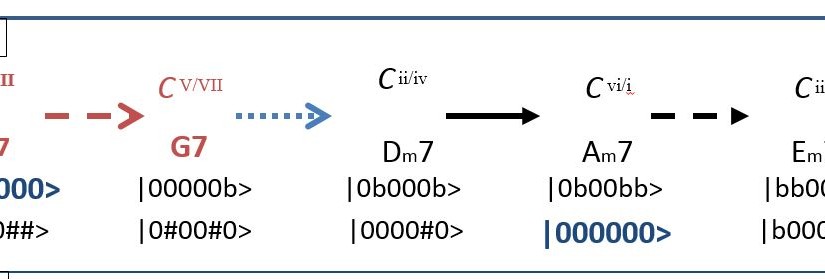
To start, lets consider what a key change would look like from C to G
staff notation
C ionian –P5–> G ionian
Cion + P5 = Gion
Where “–P5–>” stands for “change the key by an ascending fifth”. We set the convention that going with the arrow is an ascending fifth while going against the arrow is an ascending fourth.
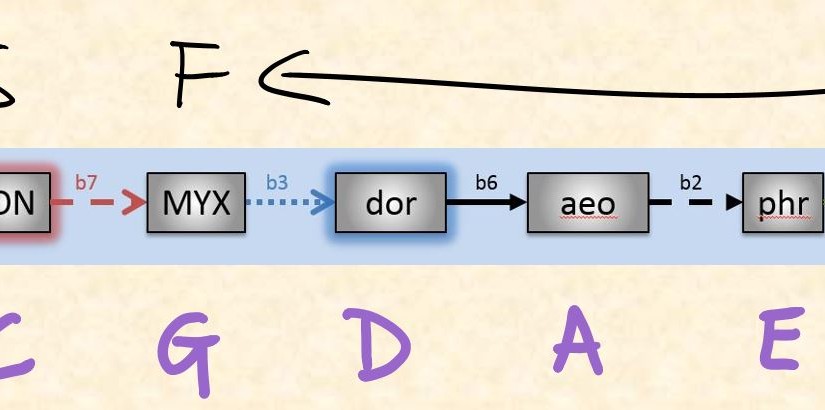
Now consider the transition from C ionian to C mxyolydian; it only involves a flattening the seventh degree (an operation we will annotate as b7 from now on). As an accidental network, this looks like
C Ionian –b7–> C Myxolydian
Where going with the arrow means you flat the seven while going against the arrow means you sharp the seven.
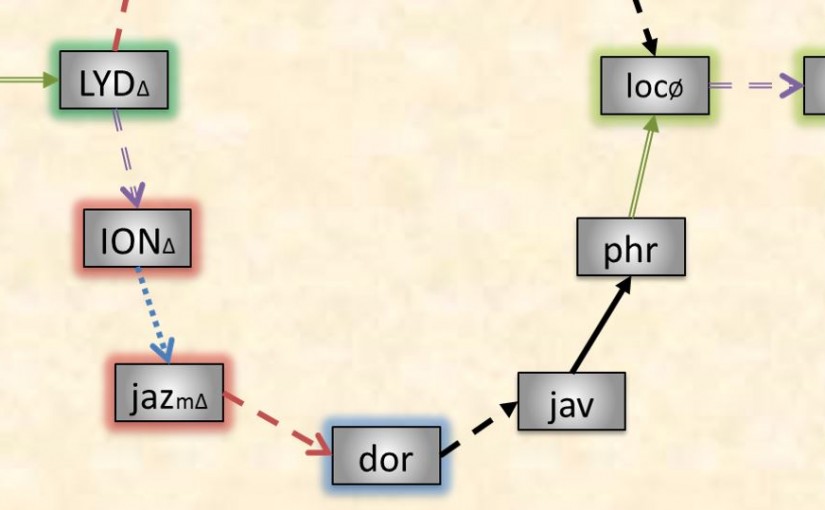
If we now wish to transition from C ionian to G myxolydian and thus remain diatonic, the accidental network would look like this
C Ionian — P5 –> G ionian — b7 –> G myxolydian
As stated in the accidental abacus, we can combine the P5 and b7 operation into an accidental jump. There is one accidental jump associated with each scale degree. We denote a “forward jump” as one that goes with the stated arrow and corresponds to a perfect fifth key change. We denote a “backward jump” as the opposite, going against the arrow and corresponding to a perfect fourth jump.
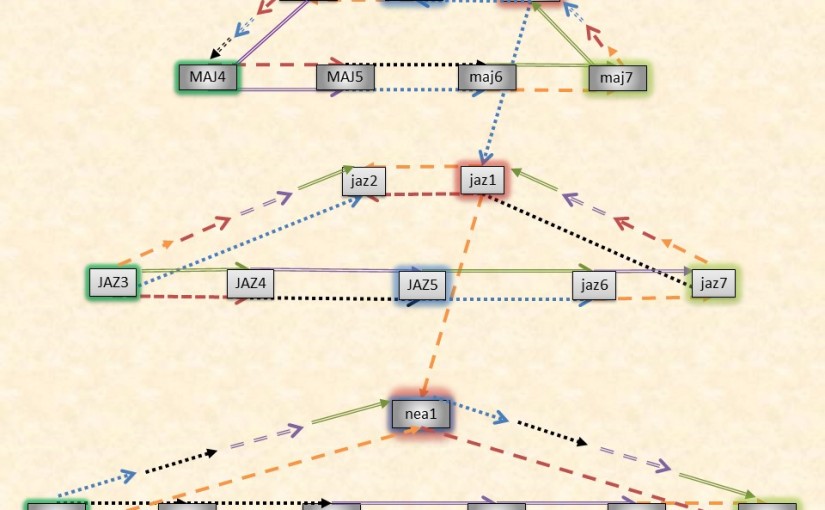
An open accidental network is one in which there is no link from the first mode to the last. For example, the accidental network in going from C ionian to G myxolydian to D dorian is:
diagram
Notice that there is no link connecting D dorian with C ionian thus making this an open network. The links in an open network will always be accidental jumps and thus correspond to perfect fifth key change movements. Open networks seem to be only useful for theoretical discussion and pedagogy given that the two most important structures in music theory, the scale and the circle of fifths, both have their last mode connecting with their first, i.e. closed.
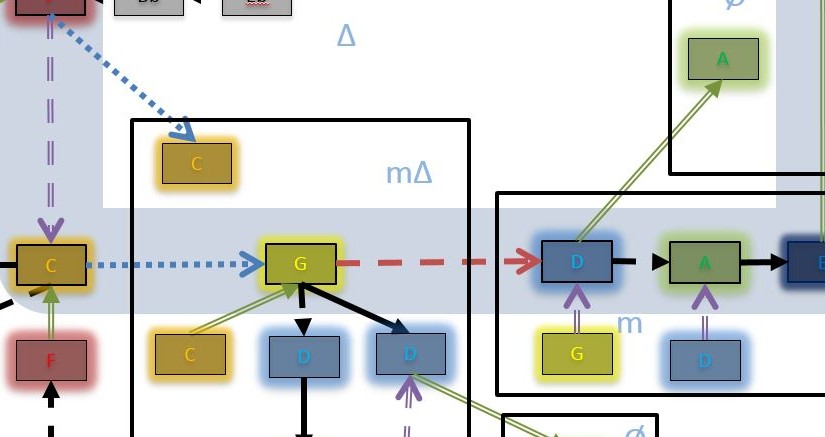
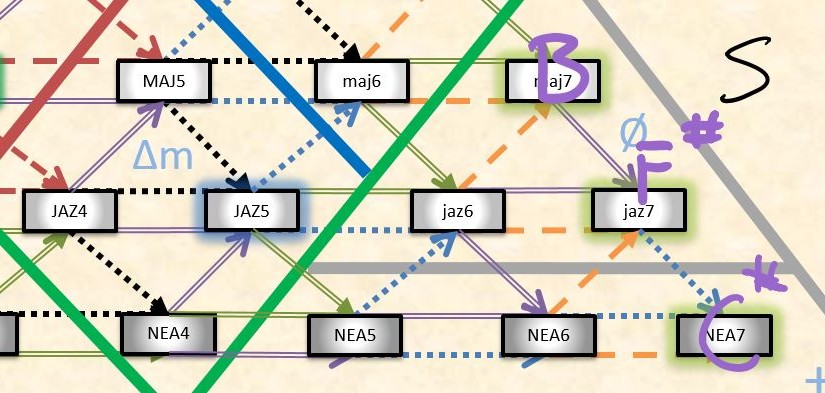
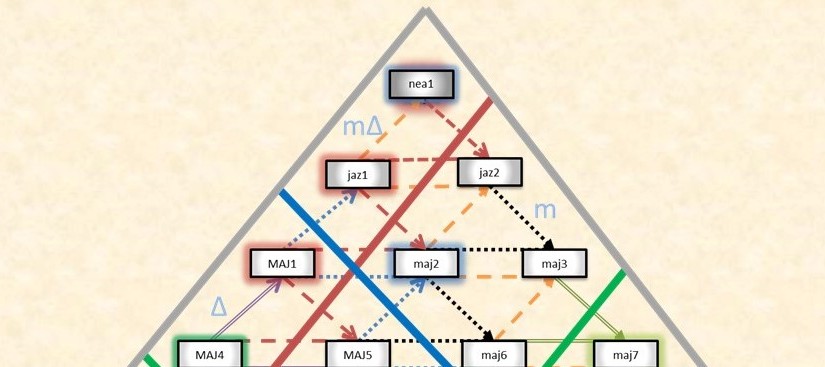
There are two types of closed networks: rings and wheels. In each case, the last mode has a link that connects it to the first mode. The difference lay in the type of links and modes allowed. In a ring, we only use diatonic sets of modes but allow the links to represent any intervals. In a wheel, we use only non-diatonic sets of modes but the links must be exclusively accidental jumps. Let us examine several examples to better understand the different networks. Notice that by this definition, the basic construct of the accidental network, two modes connected by one lin
Open Networks