- The accidental abacus is a visualization of the heptatonic modes. It consists of a 7×2 grid and six elements within it corresponding to the six non-root scale degrees of a mode. Moving any of these elements to the left represents a flattening of that scale degree; a movement to the right, a sharpening.
A conventional abacus uses sliding beads on sets of wires in order to annotate numbers and perform calculations.


Japanese and Chinese abaci.
In an abacus, the positions of the beads on a particular wire denote a particular power in a number. Thus moving one bead on one particular wire may mean to add one while moving a bead on another wire may mean to add ten. If the abacus started at zero each time, then the moving one bead represents the number ten and moving two beads the number ten.
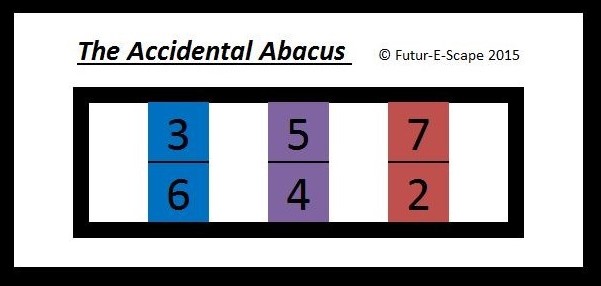
In the accidental abacus we use this approach to create a hypothetical abacus in which the beads are the scale degrees and movement is restricted to flattening or sharpening that scale degree by moving it left or right once respectively.
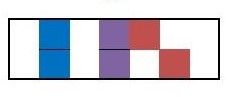
Ionian mode of the major scale.
The above is the abacus in its natural state; there are no flat or sharp’s and every scale degree is in a natural position. This therefore represents the ionian state of the major mode. If we now wished to represent a different mode within our abacus, then we would have to shift the scale degrees to accommodate the accidental spelling of our new mode.
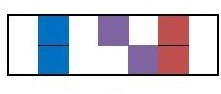
For example, if we wish to represent the myxolydian mode within our abacus, then we would have to have it represent a state with a flattened 7th degree which corresponds to the accidental spelling of the myxolydian mode. This would be represented on our abacus as follows:
 Myxolydian
Myxolydian
In this case, we could go from C ionian to C myxolydian by doing nothing more than flattening the seven. However, to stay diatonic, we must actually be in the key of G and then flat the seven to be in G myxolydian. The next smallest movement in the major scale would correspond to sharpening the four which transitions us from the ionian to the lydian mode:
Lydian
As before, we can go from C ionian to C lydian with nothing more than a shappening of the fourth but to stay diatonic we must first move to the key of F and then sharp the fourth.
Myxolydian and lydian are the only major modes requiring a single accidental shift from ionian. We draw attention to the pattern that flattening an scale degree also required a perfect fifth key center change to stay diatonic while sharpening a scale degree required a perfect fourth key center change to stay diatonic. The melding of a flat scale degree shift to a perfect fifth key center change and a sharp scale degree shift to a perfect fourth key center change is consistent among all modes in all scale. In the interests of clarity, we will adopt the convention of calling any key center change in fourth or fifth a jump and any flattening, sharpening, or naturalizing of a scale degree as an accidental operation. That an accidental operation must also have a jump to remain diatonic is a fundamental tenant of orijikan and we will refer to these combined operations as accidental jumps.
In order to further familiarize ourselves with the accidental abacus as well as lend weight to the idea of an accidental jump, let us examine a mode that requires two accidental operations:

Dorian
In this case, we see that we have had to flatten the third and seventh scale degree in order to go from the ionian mode to the dorian mode. If we interpret the above as accidental jumps, then we have two flat jumps required to go from the all-natural spelling of the ionian mode to the two accidental spelling of the dorian mode. Two flat jumps would correspond to two perfect fifth jumps within our model. Since each perfect fifth jump is comprised of 7 half-steps, then two jumps would span 14 half-steps. But due to octave equivalence, taking 12 half-steps returns us to the start and thus we had actually only netted a total of 2 half-steps form our starting position. If we take C ionian as our default and wished to go to dorian and remain diatonic, then 2 half-steps would take you to the key of D at which point you would flat the third and seventh degree giving you D dorian.
Below, we list all the modes of the major scale. The left column represents the major scale in steps ( whole and halfs), while the right column represents the major scale in jumps (perfect fifth and a tritone, which is 6 perfect fifths):
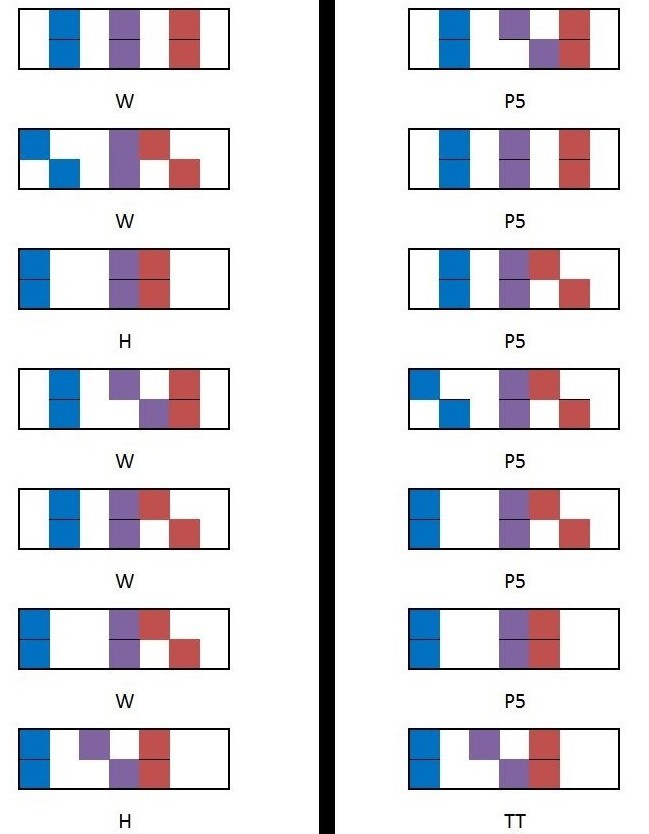
Major scale in steps and fifths as represented by the accidental abacus
On the left, we clearly see the pattern that when two scale degrees are flattened (such as going from Ionian to dorian and the dorian to phrygian), we obtain a whole step but when five degrees are sharpened (such as going from phrygian to lydian and locrian to ionian), we obtain a half-step. This is again consistent considering that the sharpening of five scale degrees corresponds to five sharp accidental jobs. Each sharp accidental jump is a perfect fourth jump which consists of five half-steps. Thus five sharp jumps correspond to 25 half steps or 1 half-step due when octave equivalence is applied. This then accounts for the “whole whole half whole whole whole half” spelling of the major scale.
On the right, we see the exact same modes for the exact same scale but now arranged in terms of a singular flat jumps and one sharp jump, the tritone. Thus we see that starting with the lydian and ending with locrian, we have a chain of singular jumps which connect all the modes of the major scale. The final jump connecting locrian back to lydian is a tritone. But it is still acceptable say that there are only perfect fifth jumps within this model considering that six simultaneous fifth jumps would equal forty-two half-steps or six half-steps, a tritone, after octave equivalence.
The purpose of this essay is merely to introduce the accidental abacus and its usage. We leave our further discussion on its application and discussions of the patterns within it for future essays as well as the commentary below.